标定目的
首先,我们必须要明确一个问题:为什么需要对摄像头进行标定?
在计算机视觉领域,我们是将三维物体转换到二维平面,这就需要确定空间物体表面某点的三维几何位置与其在二维图像中对应点之间的相互关系,这又需要建立摄像头成像的几何模型,而这些几何模型的参数就是摄像头参数,包括内参、外参、畸变参数等。
而我们进行标定的目的:求出摄像头的内、外参数,以及畸变参数,进而可以建立摄像头成像的几何模型。
总之,就是寻找图像和现实的数学转换关系,从而可以从图像中测量出实际数据,而在标定完成之后,一般会做两件事:
- 由于每个镜头的畸变程度不同,导致成像时的图像会内凹或者外凸,通过标定可以矫正这种镜头畸变,让摄像头能够正确生成矫正后的图像
- 根据获得的图像重构三维场景,即三维重建,使用同一成像几何模型下的多视角二维图像来拟合出三维信息,可以认为是标定的逆过程
那么,是不是所有的摄像头都需要标定呢?答案是否。简单来说,像自动驾驶感知摄像头都是需要标定的,因为算法需要提取图像中的信息(物体类别、物体尺寸等)并将该信息参与计算,如果不进行标定工作,那么得到的视野信息就会有误,无法对物体、距离进行准确的判断,而类似于RVM摄像头(倒车影像)、监控摄像头这种类型的摄像头,它的作用仅仅是用于显示图像给人观察,图像信息并不会参与后续的计算,所以无需标定。
在介绍标定原理前,我们先介绍摄像头成像原理、四个坐标系、摄像头参数。
标定原理
成像原理
我们以最常见的相机为例,相机的成像原理就是小孔成像原理,后续的所有公式推导均是基于该原理进行的。通过该原理我们可以建立模型——针孔模型,如下图所示。
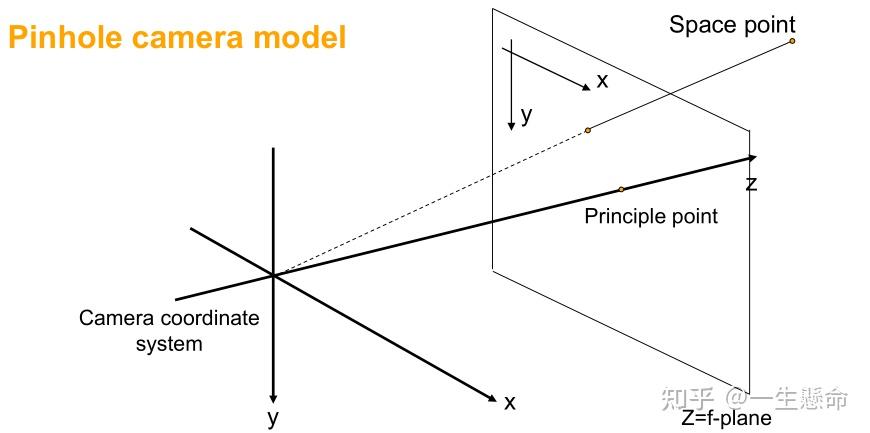
左侧是相机坐标系,右侧是图像平面,相机所在位置为原点,也是成像小孔所在位置,图像平面与小孔的距离为焦距 f ,焦距的物理意义是:当图像平面与相机距离为 f 时,成像最清晰。 Z 轴为光轴,它垂直于相机平面和图像平面,与图像平面的交点叫主点(Principle point)。
以针孔模型为基础的坐标变换示意图如下,涉及到四个坐标系:像素坐标系、图像坐标系、相机坐标系、世界坐标系。
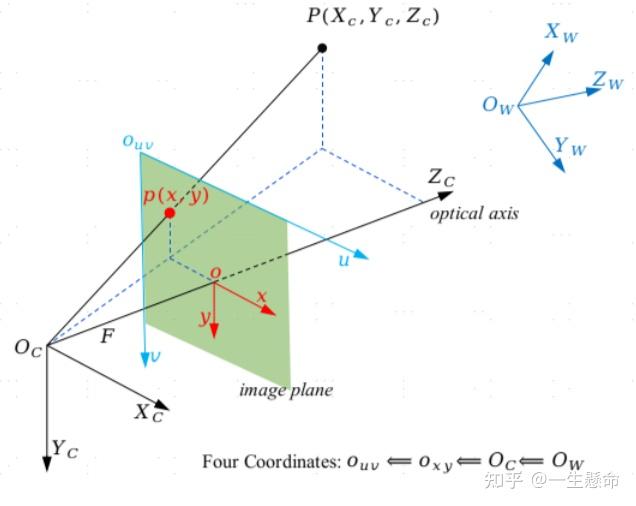
总之,相机成像的原理本质上就是三维空间坐标到二维空间坐标的变换。所以标定的目的就是**确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,建立摄像头成像的几何模型,这些几何模型参数就是摄像头参数。**所以求出摄像头的参数,我们也就基本完成了标定过程。接下来我们介绍4个坐标系。
四个坐标系
像素坐标系$(u,v)$
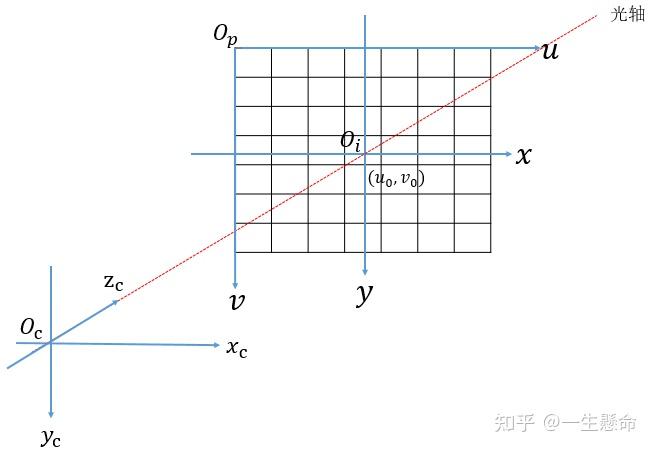
下图便是像素坐标系,像素的坐标就是像素在图像中的位置,水平方向为 $u$ 轴,垂直方向为 $v$ 轴,左上角为顶点 $Op$ ,也被称为远点。像素坐标系反映了摄像头/相机的感光元件(CCD/CMOS)中像素的排列情况,坐标轴单位为像素(Pixel),可以认为一个小方格就代表一块像素。
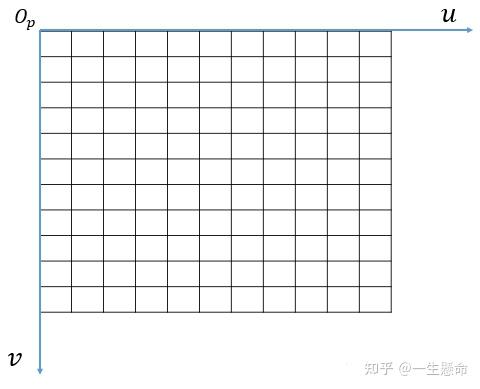
在像素坐标系中,任意一个像素坐标可以表示为 $(u_i,v_i)$ 。
- 图像坐标系$(x,y)$
像素坐标系下,每个像素的坐标是由像素表示的,但是这种表示方法不能反应图像物体的尺度大小,所以我们需要将像素坐标转换为图像坐标,方法如下:
将像素坐标系的原点平移到图像中心,并将中心位置定位图像坐标系的原点 $O_i$ (即图像中心点),图像坐标系的 x 轴与像素坐标系的 u 轴平行且同向, y 轴与 v 轴平行且同向。我们一般描述像素点都是几行几列,所以二者的转换关系为:其中dx和dy表示每一行和每一列分别代表多少mm,即1 pixel=dx mm。
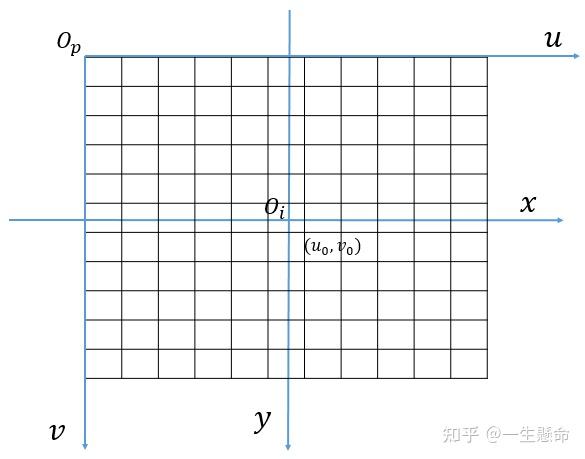
- 摄像头坐标系(相机坐标系)$(x_c,y_c,z_c)$
摄像头坐标系也叫相机坐标系,以摄像头的光轴为 z 轴,光线在摄像头光学系统的中心位置(镜头的光心处)就是原点 Oc,相机坐标系的水平轴 xc 和垂直轴 yc 分别和图像坐标系的 x 轴和 y 轴平行,如下图所示,可以发现,相机坐标系是三维坐标系,之前的像素、图像坐标系均为二维坐标系。其中,相机坐标系的原点 Oc 与图像坐标系原点 Oi 连线距离 $O_cO_i=f$ ,也就是摄像头焦距。
- 世界坐标系$(X_w,Y_w,Z_w)$
世界坐标系表达了图像和现实中的真实物体之间的一个映射关系,以此为基准可以描述相机与物体的空间位置,通过世界坐标系转换,我们可以将物体映射在图像中。对于单目视觉而言,就是真实物体尺寸和图像尺寸的映射关系。对于多目视觉而言,就需要明确各个摄像头之间的位置关系,然后将其转换在同一个坐标系下进行计算。世界坐标系如下图所示,原点为 Ow 。
当确定唯一且不变的世界坐标系后,后续所有的坐标系都可以通过坐标变换来获得,而当平移或旋转世界坐标系后,通过转换关系可以迅速得到图像在其他坐标系下的信息。
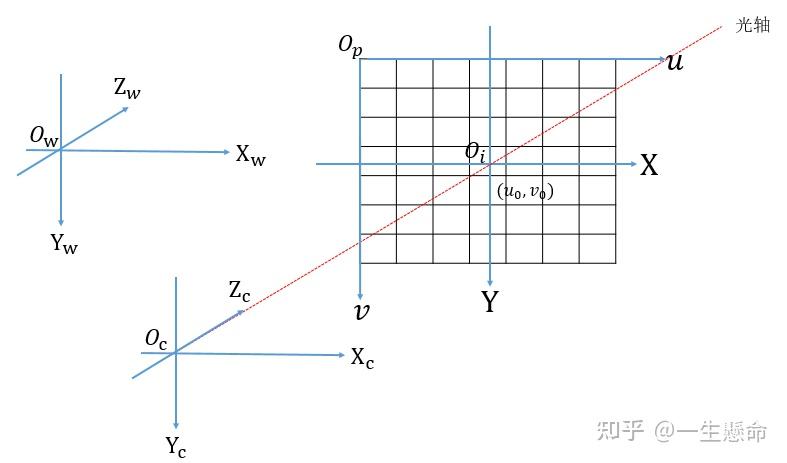
图12 世界坐标系
注意: $X_w,Y_w,Z_w$ 轴并不是和其他坐标系的坐标轴平行,而是存在一定的角度和平移关系。
从世界坐标系变换到相机坐标系属于刚体变换,即物体不会发生形变,只需要对坐标系进行平移和旋转,当对相机坐标系设定一定的参数,分别绕着 X,Y,Z 轴做平移和旋转后,就可以得到在世界坐标系的坐标。