常见的数据结构包括数组、链表、栈、队列、树和图等。每种数据结构都有其特定的优势和应用场景。例如，数组适用于索引访问和快速查找，链表适用于插入和删除操作频繁的情况，树适用于层次结构数据的表示和搜索，图适用于表示复杂的关系网络等。
1、数组
数组是将具有相同类型的若干变量有序地组织在一起的集合，可以说是最基本的数据结构。
优点： （1）按照索引查询元素的速度很快；
（2）按照索引遍历数组也很方便。
缺点： （1）数组的大小在创建后就确定了，无法扩容：定义（初始化）必须给定数据的大小；
（2）数组只能存储一种类型的数据；
（3）添加、删除元素的操作很耗时间，因为要移动其他元素。
2、栈（电梯）
栈是一种特殊的线性表，它只能在一个表的一个固定端进行数据结点的插入和删除操作。栈按照先进后出或后进先出的原则来存储数据，也就是说，先插入的数据将被压入栈底，最后插入的数据在栈顶，读出数据时，从栈顶开始逐个读出。栈在汇编语言程序中，经常用于重要数据的现场保护。栈中没有数据时，称为空栈。
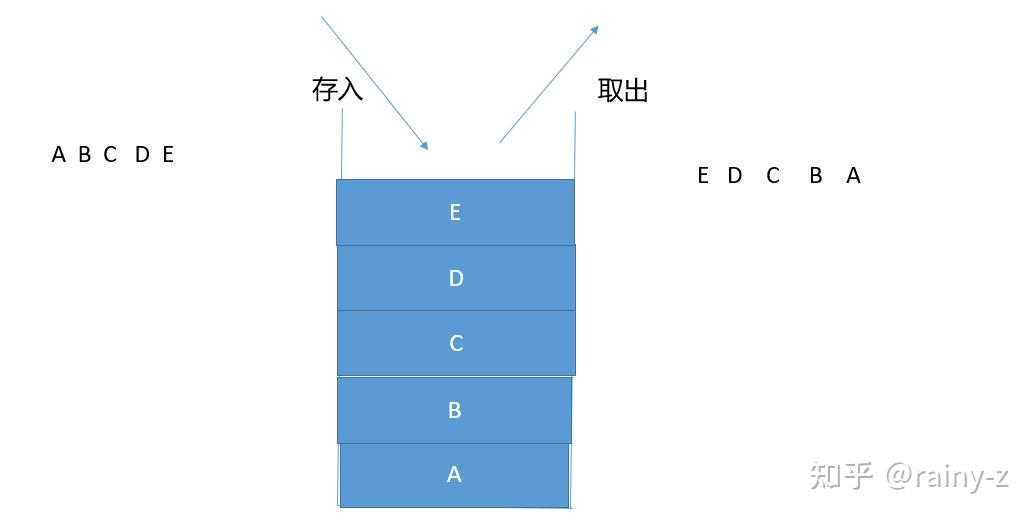栈的操作规则：后进先出
3、队列（食堂排队）
队列和栈类似，也是一种特殊的线性表。和栈不同的是，队列只允许在表的一端进行插入操作，而在另一端进行删除操作。一般来说，进行插入操作的一端称为队尾，进行删除操作的一端称为队头。队列中没有元素时，称为空队列。
队列的操作规则：先进先出
为了提高队列的利用率，采用循环队列来存储数据循环队列: rear 加到 顶时 回来。
4、链表
链表是一种数据元素按照链式存储结构进行存储的数据结构，这种存储结构具有在物理上存在非连续的特点。链表由一系列数据结点构成，每个数据结点包括数据域和指针域两部分。其中，指针域保存了数据结构中下一个元素存放的地址。链表结构中数据元素的逻辑顺序是通过链表中的指针链接次序来实现的。
链表分为单向链表、双向链表和循环列表。
1）单向链表
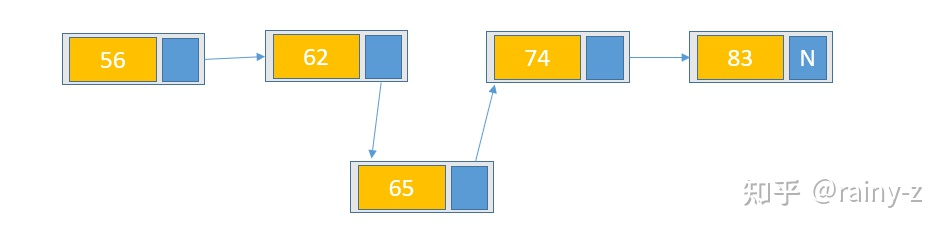前面的黄色方块代表数据域，后面蓝色方块是指针域。
2）双向链表
p代表prev，N代表next。
3）单向循环链表
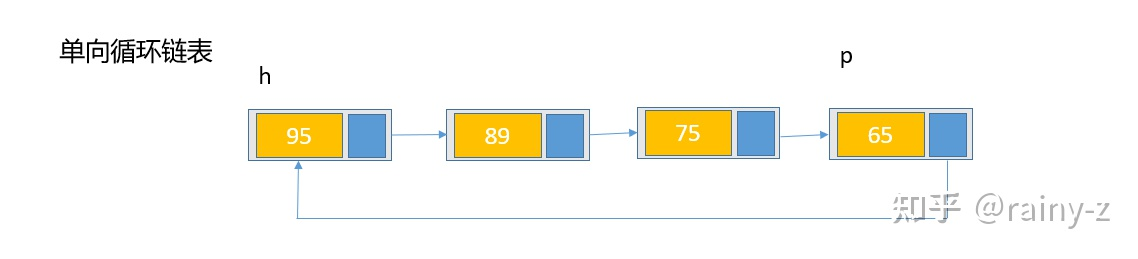h是头结点，p是定义的一个指针
单向链表的缺点是只能从头到尾依次遍历，而双向链表可进可退，既能找到下一个，也能找到上一个，每个节点上都需要多分配一个存储空间。
5、树
树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。树是典型的非线性结构，在树结构中，有且仅有一个根结点，该结点没有前驱结点。在树结构中的其他结点都有且仅有一个前驱结点，而且可以有两个后继结点。
二叉树 二叉树特点:
- 二叉树第i（i≥1）层上的节点最多为2^i-1个
- 深度为k（k≥1）的二叉树最多有2^k - 1个节点
- 在任意一棵二叉树中，树叶的数目比度数为2的节点的数目多1
二叉树遍历 二叉树中还包括满二叉树和完全二叉树。
满二叉树 ：深度为k（k≥1）时有2k－1个节点的二叉树。
完全二叉树 ：只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。
完全二叉树的判断
6、图
图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。如果两个顶点之间存在一条边，那么就表示这两个顶点具有相邻关系。
图分为有向图和无向图：
有向图：边不仅连接两个顶点，并且具有方向； 无向图：边仅仅连接两个顶点，没有其他含义；
7、堆
堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：
堆中某个结点的值总是不大于或不小于其父结点的值； 堆总是一棵完全二叉树。 将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
大根堆
小根堆
8、散列表（哈希表）（字典）
散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里，这种存储空间可以充分利用数组的查找优势来查找元素，所以查找的速度很快。
哈希查找有3个概念
1 、关键字 (key)
2 、计算公司(哈希函数 又称为 散列函数)
3 、存储数据的表 (哈希表又称为 散列表)
算法(哈希函数)：
直接寻址法：取关键字或关键字的某个线性函数值为散列地址。 数字分析法：通过对数据的分析，发现数据中冲突较少的部分，并构造散列地址。例如同学们的学号，通常同一届学生的学号，其中前面的部分差别不太大，所以用后面的部分来构造散列地址。 平方取中法：当无法确定关键字里哪几位的分布相对比较均匀时，可以先求出关键字的平方值，然后按需要取平方值的中间几位作为散列地址。这是因为：计算平方之后的中间几位和关键字中的每一位都相关，所以不同的关键字会以较高的概率产生不同的散列地址。 折叠法：将关键字分割成位数相同的几部分，最后一部分位数可以不同，然后取这几部分的叠加和（去除进位）作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐，然后相加；间界叠加是从一端向另一端沿分割界来回折叠，然后对齐相加。 取随机数法：使用一个随机函数，取关键字的随机值作为散列地址，这种方式通常用于关键字长度不同的场合。 除留取余法：取关键字被某个不大于散列表的表长 n 的数 m 除后所得的余数 p 为散列地址。这种方式也可以在用过其他方法后再使用。该函数对 m 的选择很重要，一般取素数或者直接用 n。